 Exit Help
Exit Help
Extrasolar Planetary Satellite Integrator Help File
Star & Planet Information
HELP. Displays this help screen. To exit, click one of the
Exit Help buttons located at the
top and bottom of this screen.
STELLAR MASS. Specify the mass of the star that the extrasolar
planet revolves around in units of Solar masses. Sunlike stars have
masses near 1.0.
PLANETARY MASS. Specify the mass of the extrasolar planet in in
units of Jupiter masses. Extrasolar planets have masses that range
from 0.5-10 Jupiter masses.
PLANET RADIUS. Specify the radius of the extra-solar planet in
Jupiter Radii. This parameter is not known for most extrasolar
planets, 1.0 is a good estimate.
PLANETARY SEMIMAJOR AXIS. Specify the semimajor axis of the
orbit of the extrasolar planet in Astronomical Units (AU). The
distance from the Earth to our Sun is 1.0 AU. Extrasolar planets
discovered to date range from 0.04 - 3.0AU.
PLANETARY ECCENTRICITY. Specify the eccentricity of the orbit
for the extra-solar planet. This is a measure of ellipticity which
ranges from 0 to 1. A value of 0.0 is a perfect circle, with larger
values representing successivly more elongated ellipses.
Integration Parameters
ACCURACY. This number specifies the accuracy of the
integration. More accurate integrations take longer and are more prone
to run into numerical problems. Accordingly, you want the lowest
number which gives an accurate plot. Experiment by following the same
orbit at different accuracies and seeing if the output plots are
similar.
INTEGRATION TIME. Here you specify how many years into the future
the orbit should be followed. Be careful in choosing this parameter as
it is directly correlated to how long you will wait before seeing a
plot! A good strategy is to try a short integration time first to get
an idea of how fast the program is.
FREQUENCY. This number determines how often a point along the
orbit is saved to disk. A larger number yields a more accurately drawn
orbit at the expense of plotting time and disk space. You want to
choose the largest number that yields a reasonably accurate
orbit. Experiment!
INTEGRATION LIMITS. These upper and lower limits on the
planet-satellite distance allow you to stop the integration once the
satellite has wandered into an uninteresting regime. Less than 1.0
planetary radii corresponds to a collision, while greater than several
hundred to several thousand radii correspond to a satellite which
escapes the planet.
Initial Conditions
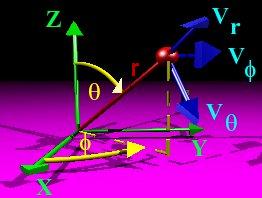
INITIAL POSITION. The initial position needs to be specified in
spherical coordinates where r is length of the radius vector, θ
is the angle between the z-axis and the radius vector, and φ is
measured from the x-axis to the projection of the radius vector into
the xy plane (see figure). Valid Ranges: r > 0, 0 ≤ θ ≤ 180
degrees, -180 ≤ φ ≤ 360 degrees.
INITIAL VELOCITY. The initial velocity is specified in a local
coordinate system based on the particle's position. The velocities
vr, vθ, and vφ are in the
directions that would cause r, θ, and φ to increase (see
figure). Since the velocities are normalized to the circular velocity,
when the total speed is 1.0, the satellite starts on an initially
circular orbit around the planet. The total velocity squared is the
sum of the squares of the three velocity components.
SUBMIT FORM. Send the parameters that you have chosen to the
orbital integration program!
LOAD DEFAULTS. Default values are for the first transiting extrasolar
planet: HD 209458.
 Exit Help
Exit Help

 Exit Help
Exit Help

 Exit Help
Exit Help